二分查找

1、lc74-搜索二维矩阵

https://leetcode.cn/problems/search-a-2d-matrix/description/?envType=study-plan-v2&envId=top-100-liked

  • 二维数组下标与一维数组下标的映射
  • 取mid坐标防止溢出的写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int l = 0, r = m * n - 1; // 将二维矩阵看作长度为 m*n 的一维数组
        while(l <= r){
            int mid = l + (r - l) / 2;// 和 (l + r) / 2 结果相同，但养成这样的习惯可以防止溢出
            int mVal = matrix[mid / n][mid % n]; // 转换回二维坐标

            if(mVal == target) return true;
            if(mVal < target) l = mid + 1;
            if(mVal > target) r = mid - 1;
        }

        return false;
    }
}

2、lc34-在排序数组中查找元素的第一个和最后一个位置

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/?envType=study-plan-v2&envId=top-100-liked

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int n = nums.length;
        int min = -1, max = -1;
        
        int l = 0, r = n - 1;
        //找左边界
        while(l <= r){
            int m = l + (r - l) / 2;

            if(nums[m] >= target) r = m - 1;//往左逼，相等时也要往左逼
            else l = m + 1;

            if(nums[m] == target) min = m;//每次相等都会先记录一次
        }
        //找右边界
        l = 0;
        r = n - 1;
        while(l <= r){
            int m = l + (r - l) / 2;

            if(nums[m] <= target) l = m + 1;
            else r = m - 1;

            if(nums[m] == target) max = m;
        }

        return new int[]{min, max};
    }
}

3、lc33-搜索旋转排序数组

https://leetcode.cn/problems/search-in-rotated-sorted-array/description/?envType=study-plan-v2&envId=top-100-liked

  • 将数组从中间分成左右两部分，一定有一部分数组是有序的
  • 根据有序的那部分确定该如何改变上下界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        int l = 0, r = n - 1;
  
        while (l <= r) {
            int mid = (l + r) / 2;
            // 命中直接返回
            if (nums[mid] == target) {
                return mid;
            }

            //每次都要分，分出哪部分是有序的，有序的才可以用二分思想缩小边界
            if (nums[0] <= nums[mid]) { // 要有等于号
                //判断了哪部分是有序数组才能用二分，在有序数组中才能用二分
                //然后确定target是否在有序区间这里
                if (nums[0] <= target && target < nums[mid]) { // target在有序区间这
                    r = mid - 1; // 将范围缩小到这个区间
                } else { // target不在有序区间这
                    l = mid + 1;  //将范围缩小到另一个区间，下一次while循环又会将这个区间分成有序和无序
                }
            } else { 
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }

        return -1;
    }
}

4、lc153-寻找旋转排序数组中的最小值

https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/description/?envType=study-plan-v2&envId=top-100-liked

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int findMin(int[] nums) {
        int n = nums.length;
        int l = 0, r = n - 1;
        // 不是找目标值，无需一直找下去直到 l == r
        // 当 l == r 时就是最小值的位置了，就不能再进去循环改变 l 和 r 的值了
        while(l < r){ 
            int m = l + (r - l) / 2;

            // 不是找目标值，模板稍微有些不同
            // 通过 nums[m] 和 nums[r] 的大小关系来判断最小值在哪边
            if(nums[m] < nums[r]){
                //最小值在左边的区间（包含 m）
                r = m; // 缩小区间
            }else{ // 否则在右边的区间
                l = m + 1;
            }
        }

        return nums[l];
    }
}

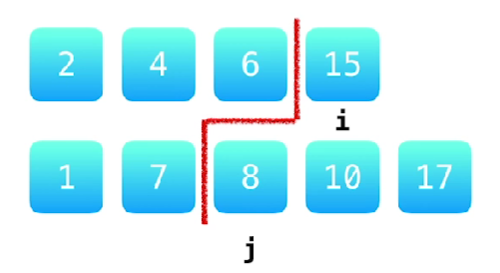
5、lc4-寻找两个正序数组的中位数

https://leetcode.cn/problems/median-of-two-sorted-arrays/description/?envType=study-plan-v2&envId=top-100-liked

image-20251111092205333

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        // 确保 nums1 是较短的数组
        if (nums1.length > nums2.length) {
            return findMedianSortedArrays(nums2, nums1);
        }

        int m = nums1.length;
        int n = nums2.length;
        // 二分的「边界」不是数组下标，而是“分割线的位置”，所以要取到 m
        int left = 0, right = m;
        // LMax 表示左半部分的最大值
        // RMin 表示右半部分的最小值
        int LMax = 0, RMin = 0;

        // 在较短的数组 nums1 上进行二分查找
        while (left <= right) {
            // i 为 nums1 的分割点，左边有 i 个元素
            // 在较短的数组上确定分割线的位置，保证分割线两边两个数组都有元素，防止下标越界
            int i = (left + right) / 2; 
            // j 根据总长度确定，使左半部分元素个数为 (m + n + 1) / 2
            // 确保时刻都满足找中位数的数量关系：整体左半部分的元素个数等于右半部分的元素个数（或多一个）
            int j = (m + n + 1) / 2 - i;

            // 取分割线两侧关键值，注意边界情况
            int nums1LMax = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]); // nums1 左边最大值
            int nums1RMin = (i == m ? Integer.MAX_VALUE : nums1[i]);     // nums1 右边最小值
            int nums2LMax = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]); // nums2 左边最大值
            int nums2RMin = (j == n ? Integer.MAX_VALUE : nums2[j]);     // nums2 右边最小值

            // 满足部分条件，要继续往右逼找到最大满足条件的 i
            if (nums1LMax <= nums2RMin) {
                // 更新当前的左半部分最大值和右半部分最小值
                LMax = Math.max(nums1LMax, nums2LMax);
                RMin = Math.min(nums1RMin, nums2RMin);
                // i 右移，尝试让 nums1 多分一些元素给左半部分
                left = i + 1;
            } else {
                // 若 nums1LMax > nums2RMin，说明 i 太大，应向左收缩
                right = i - 1;
            }
        }

        // 根据总长度奇偶性返回中位数
        return (m + n) % 2 == 0 ? (LMax + RMin) / 2.0 : LMax;
    }
}