2025-11-06

回溯法

1、理论基础

应用场景

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

如何理解回溯法

回溯的本质是穷举，穷举所有可能，选出我们想要的答案
回溯法解决的问题都可抽象为树形结构
回溯法解决的问题都是在集合中递归查找子集
集合的大小构成了树的宽度，递归的深度构成树的深度
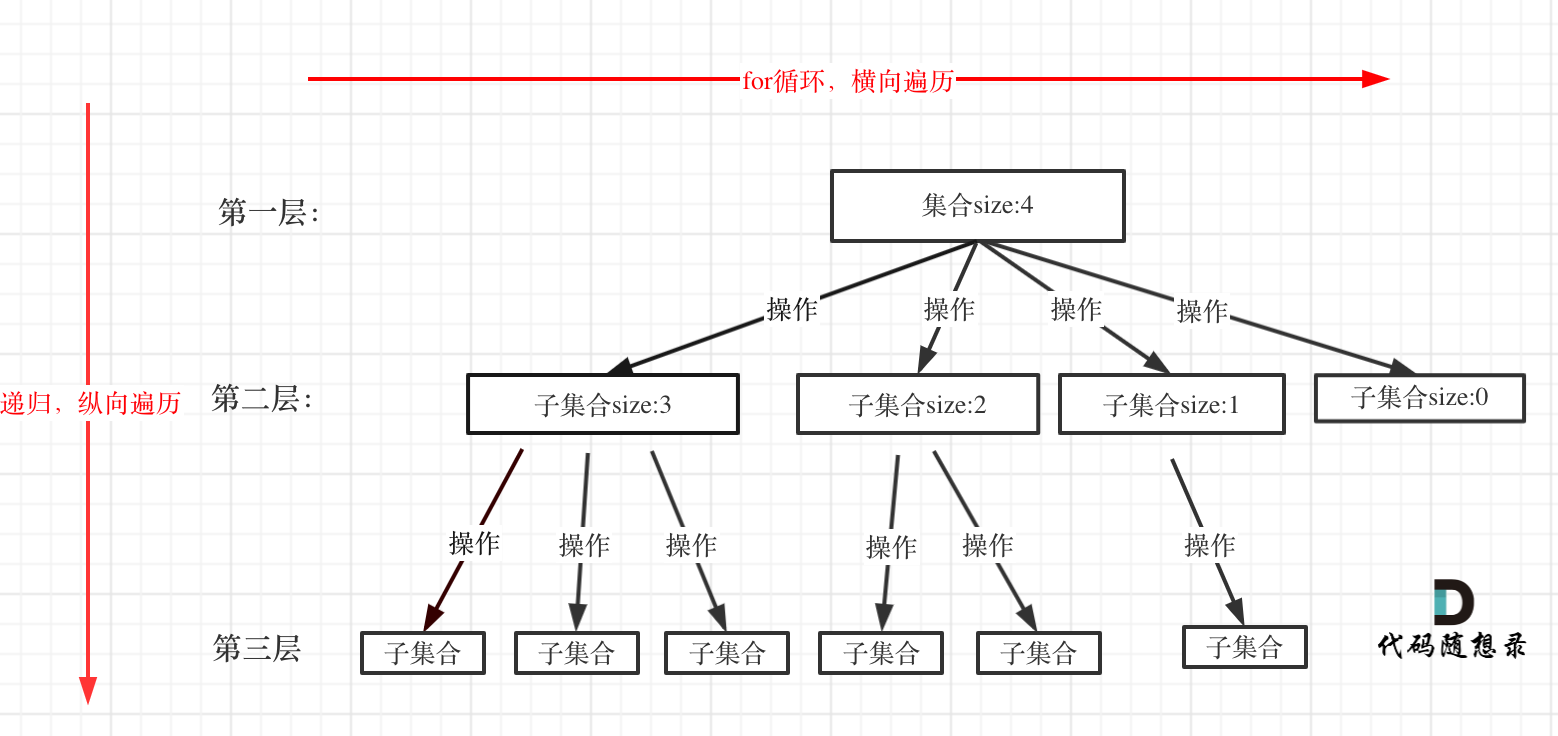
for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历

模板：

void backtrack(参数) {
    if (找到一个结果的终止条件) {
        存放单次结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点/处理单次结果;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

2、lc77-组合

原题链接：https://leetcode.cn/problems/combinations/

回溯法用递归来解决嵌套for循环层数的问题
每一次的递归中一个for循环，那么递归就可以用于解决多层嵌套循环的问题

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k, 1);
        return res;
    }

    public void backtrack(int n, int k, int si){
        if(path.size() == k){
            res.add(new ArrayList<>(path));
            return;
        }


        for(int i = si; i <= n; i++){
            path.add(i);
            backtrack(n, k, i + 1);
            path.remove(Integer.valueOf(i));
        }
    }
}

剪枝优化版

如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        combineHelper(n, k, 1);
        return result;
    }

    /**
     * 每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex
     * @param startIndex 用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
     */
    private void combineHelper(int n, int k, int startIndex){
        //终止条件
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
            path.add(i);
            combineHelper(n, k, i + 1);
            path.remove(Integer.valueOf(i));
        }
    }
}

3、lc46-全排列

组合无序，排列有序

https://leetcode.cn/problems/permutations/?envType=study-plan-v2&envId=top-100-liked

因为排列问题每次都要从头开始搜索（因为排列是有序的，这样才能得到所有排列的可能），因此可能会遍历到已使用过的元素（一个排列里一个元素只能使用一次）。而 used数组 就是拿来记录此时path里都有哪些元素使用了

class Solution {
    List<Integer> path = new ArrayList<>();
    List<List<Integer>> res = new ArrayList<>();
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        used = new boolean[nums.length];
        backtrack(nums);
        return res;
    }

    public void backtrack(int[] nums){
        int n = nums.length;
        if(path.size() == n){
            res.add(new ArrayList<>(path));
            return;
        }

        for(int i = 0; i < n; i++){
            if(used[i]) continue;
            
            used[i] = true;
            path.add(nums[i]);
            backtrack(nums);
            path.remove(Integer.valueOf(nums[i]));
            used[i] = false;
        }
    }
    
}

4、lc78-子集

https://leetcode.cn/problems/subsets/description/?envType=study-plan-v2&envId=top-100-liked

组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点
无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始

class Solution {
    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    List<Integer> path = new ArrayList<>();// 用来存放符合条件结果
    public List<List<Integer>> subsets(int[] nums) {
        subsetsHelper(nums, 0);
        return result;
    }

    private void subsetsHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));//「遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合」。
        if (startIndex >= nums.length){ //终止条件可不加
            return;
        }
        for (int i = startIndex; i < nums.length; i++){
            path.add(nums[i]);
            subsetsHelper(nums, i + 1);
            path.remove(Integer.valueOf(i));
        }
    }
}

5、lc17-电话号码的字母组合

https://leetcode.cn/problems/letter-combinations-of-a-phone-number/description/?envType=study-plan-v2&envId=top-100-liked

本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，因此每次递归到下一层遍历都要从头开始（从 0 开始）遍历

class Solution {
    List<String> res = new ArrayList<>();
    StringBuilder path = new StringBuilder();
    public List<String> letterCombinations(String digits) {
        Map<Character, String> map = new HashMap<>();
        map.put('2', "abc");
        map.put('3', "def");
        map.put('4', "ghi");
        map.put('5', "jkl");
        map.put('6', "mno");
        map.put('7', "pqrs");
        map.put('8', "tuv");
        map.put('9', "wxyz");
        
        backtrack(map, digits, 0);

        return res;
    }

    //sI表示遍历到哪个数字了
    public void backtrack(Map<Character, String> map, String digits, int sI){
        if(path.length() == digits.length()){
            res.add(path.toString());
            return;
        }
        
        String s = map.get(digits.charAt(sI));
        for(int i = 0; i < s.length(); i++){
            path.append(s.charAt(i));
            backtrack(map, digits, sI + 1);
            path.deleteCharAt(path.length() - 1);
        }
    }
}

6、lc39-组合总和

https://leetcode.cn/problems/combination-sum/solutions/406516/zu-he-zong-he-by-leetcode-solution/?envType=study-plan-v2&envId=top-100-liked

组合问题：一个集合来求组合的话，就需要startIndex；多个集合取组合，就不用startIndex
startIndex组合是无序的，虽然本题说明可以重复选取，但最多下一层只能从当前元素的位置开始（往前），绝对是不能从下标 0 开始的（往后重新开始），所以要用到startIndex

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtrack(candidates, target, 0, 0);
        return res;
    }

    public void backtrack(int[] candidates, int target, int sum, int sI){
        if(sum == target){
            res.add(new ArrayList<>(path));
            return;
        }
        if(sum > target) return;

        for(int i = sI; i < candidates.length; i++){
            path.add(candidates[i]);
            sum += candidates[i];
            backtrack(candidates, target, sum, i); //元素可重复选取，因此传入当前位置 i
            sum -= candidates[i];
            path.remove(path.size() - 1);
        }
    }
}

7、lc22-括号生成

https://leetcode.cn/problems/generate-parentheses/solutions/192912/gua-hao-sheng-cheng-by-leetcode-solution/?envType=study-plan-v2&envId=top-100-liked

组合 / 子集 / 排列：同一层可以选择多个不同元素；括号生成：每一层只有两种固定决策：要么 '(' 要么 ')'，不需要for

class Solution {
    List<String> res = new ArrayList<>();
	StringBuilder path = new StringBuilder();
    public List<String> generateParenthesis(int n) {
        backtrack(n, 0, 0);
        return res;
    }

    public void backtrack(int n, int left, int right) {
        if (path.length() == 2 * n) {
            res.add(path.toString());
            return;
        }

        // 可以放左括号
        if (left < n) {
            path.append('(');
            backtrack(n, left + 1, right);
            path.deleteCharAt(path.length() - 1);
        }

        // 可以放右括号
        if (right < left) {
            path.append(')');
            backtrack(n, left, right + 1);
            path.deleteCharAt(path.length() - 1);
        }
    }
}

8、lc79-单词搜索

https://leetcode.cn/problems/word-search/description/?envType=study-plan-v2&envId=top-100-liked

class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length, n = board[0].length;
        // 遍历所有起点，只要有一个起点能匹配成功就返回 true
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(board, word, i, j, 0)) {
                    return true;
                }
            }
        }
        return false;
    }

    // 深度优先搜索 + 回溯
    // k 表示当前匹配到 word 的第 k 个字符
    private boolean dfs(char[][] board, String word, int i, int j, int k) {
        // 越界判断 或 当前字符不匹配，直接返回 false
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length 
            || board[i][j] != word.charAt(k)) return false;
        // 若已匹配到最后一个字符，返回 true
        if (k == word.length() - 1) return true;
       
        // 临时标记当前格子为已访问，防止重复使用
        char tmp = board[i][j]; //存下来以便回溯
        board[i][j] = '#';  // '#' 表示该格子已用过
        // 四个方向继续搜索
        boolean found = dfs(board, word, i + 1, j, k + 1) ||
                        dfs(board, word, i - 1, j, k + 1) ||
                        dfs(board, word, i, j + 1, k + 1) ||
                        dfs(board, word, i, j - 1, k + 1);
        // 回溯：恢复当前格子的原值
        board[i][j] = tmp;
        
        return found;
    }
}

9、lc131-分割回文串

https://leetcode.cn/problems/palindrome-partitioning/description/?envType=study-plan-v2&envId=top-100-liked

//回溯 + 普通判断回文串
class Solution {
    List<List<String>> res = new ArrayList<>();
    List<String> path = new ArrayList<>();
    public List<List<String>> partition(String s) {
        backtrack(s, 0);
        return res;
    }

    public void backtrack(String s, int sI){
        if(sI >= s.length()){
            res.add(new ArrayList<>(path));
            return;
        }

        StringBuilder sb = new StringBuilder(); //每层递归都单独有一个
        for(int i = sI; i < s.length(); i++){
            sb.append(s.charAt(i)); //每层递归都有自己独立的sb，因此不用撤销，撤销没影响主要是，你撤销撤销的是当层的sb，但是你回到上一层时又是上一层它自己独立的新的sb，因此只有path才有撤销的必要
            if(isPalin(sb){
                path.add(sb.toString());
                backtrack(s, i + 1);
                path.remove(path.size() - 1);
            }
        }
    }

    public boolean isPalin(StringBuilder sb){
        int l = 0, r = sb.length() - 1;
        while(l < r){
            if(sb.charAt(l) != sb.charAt(r)) return false;
            l++;
            r--;
        }

        return true;
    }
}

//回溯 + 动规判断回文
class Solution {
    List<List<String>> res = new ArrayList<>();
    LinkedList<String> path = new LinkedList<>(); //链表增删效率更高
    boolean[][] dp; // 下标从 i 到 j 的子串是否是回文
    public List<List<String>> partition(String s) {
        dp = new boolean[s.length() + 1][s.length() + 1]; // 多开一行一列保险
        char[] str = s.toCharArray();
        isPalindrome(str); // 先预处理，判断好所有子串是否是回文
        backtrack(s, 0);
        return res;
    }

    public void backtrack(String s, int sI) {
        if(sI >= s.length()){
            res.add(new ArrayList<>(path));
            return;
        }

        for(int i = sI; i < s.length(); i++){
            if(dp[sI][i]){
                path.addLast(s.substring(sI, i + 1));
                backtrack(s, i + 1);
                path.pollLast();
            }
        }
    }

    
    public void isPalindrome(char[] str) {
        int n = str.length;

        for(int i = 0; i < n; i++){ //单个字符一定是回文
            dp[i][i] = true;
        }

        for(int i = 1; i < n; i++){ // i从 1 往右走
            for(int j = i - 1; j >= 0; j--){ // j 从 i 的左边一个位置一直往左走
                if(str[i] == str[j]){
                    if(i - j == 1){ // 相等且紧邻时
                        dp[j][i] = true;
                    }else if(dp[j + 1][i - 1]){ // 相等且内子串为回文时
                        dp[j][i] = true;
                    }
                }
            }
        }
    }
}

10、lc51-N皇后

https://leetcode.cn/problems/n-queens/description/?envType=study-plan-v2&envId=top-100-liked

棋盘的宽度就是for循环的长度，递归的深度就是棋盘的高度

class Solution {
    List<List<String>> res = new ArrayList<>();
    char[][] board;
    public List<List<String>> solveNQueens(int n) {
        board = new char[n][n];
        for(char[] c : board){ //初始化棋盘
            Arrays.fill(c, '.');
        }
        backtrack(n, 0);
        return res;
    }

    public void backtrack(int n, int row){
        if(row >= n){
            res.add(array2List(board));
            return;
        }

        for(int i = 0; i < n; i++){
            if(isValid(board, row, i)){ //先判断这个位置能不能放 Q
                board[row][i] = 'Q';
                backtrack(n, row + 1);
                board[row][i] = '.';
            }
        }
    }

    public List<String> array2List(char[][] board){
        List<String> list = new ArrayList<>();
        for(char[] c : board){
            list.add(String.copyValueOf(c));
        }
        return list;
    }

    //注意别搞混行列
    public boolean isValid(char[][] board, int row, int col){ //只需往“上”检查
        //检查列
        for(int i = row - 1; i >= 0; i--){
            if(board[i][col] == 'Q') return false;
        }

        //检查上半部分主对角线
        for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--){
            if(board[i][j] == 'Q') return false;
        }

        //检查上半部分副对角线
        for(int i = row - 1, j = col + 1; i >= 0 && j < board[0].length; i--, j++){
            if(board[i][j] == 'Q') return false;
        }

        return true;
    }
}

刘文鑫

记录与分享

回溯法

1、理论基础

2、lc77-组合

3、lc46-全排列

4、lc78-子集

5、lc17-电话号码的字母组合

6、lc39-组合总和

7、lc22-括号生成

8、lc79-单词搜索

9、lc131-分割回文串

10、lc51-N皇后